FUZZY LOGIC
1. KONSEP FUZZY LOGIC
Sebelum munculnya teori logika fuzzy (Fuzzy Logic), dikenal sebuah logika tegas (Crisp Logic) yang memiliki nilai benar atau salah secara tegas. Sebaliknya Logika Fuzzy merupakan sebuah logika yang memiliki nilai kekaburan atau kesamaran (fuzzyness) antara benar dan salah. Dalam teori logika fuzzy sebuah nilai bisa bernilai benar dan salah secara bersamaan namun berapa besar kebenaran dan kesalahan suatu nilai tergantung kepada bobot keanggotaan yang dimilikinya.
a. Perbedaan Logikafuzzy dengan Logika Tegas
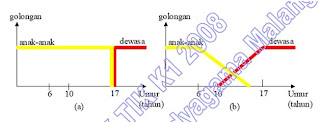
Perbedaan antara kedua jenis logika tersebut adalah: logika tegas memiliki nilai tidak=0.0 dan y=1.0. sedangakan antarn 0.0 hingga 1.0. Secara grafik perbedaan antara logika tegas dan logika fuzzy ditunjukkan oleh gambar dibawah ini:

Didalam gambar 2.1.a) apabila X leblh dan atau sama dengan 10 baru dikatakan benar yaitu bernilai Y1. sebaliknya nilai X yang kurang dan 10 adalah salah yaitu Y=0. Maka angka 9 atau 8 atau 7 dan sejenisnya adalah dikatakan salah.
Didalam gambar 2.1.b) nilai X = 9, atau 8 atau 7 atau nilai antara 0 dan 10 adalah dikatakan ada benarnya dan ada juga salahnya. Dalam contoh kehidupan kita dikatakan seseorang dikatakan sudah dewasa apabila berumur lebih dari 17 tahun. maka sesiapapun yang kurang dari umur tersebut di dalam logika tegas akan dikatakan sebagai tidak dewasa atau anak-anak. Sedangkan dalam hal ini pada logika fuzzy umur dibawah 17 tahun dapat saja dikategorikan dewasa tapi tidak penuh. misal untuk umur 16 tahun atau 15 tahun atau 14 tahun atm 13 tahun. Secara grafik dapat digambarkan sebagai berikut:
b. Himpunan Logika Fuzzy
Dalam teori logika dikenal himpunan fuzzy (fuzzy set) yang merupakan pengelompokan sesuatu berdasarkan variabel bahasa, yang dinyatakan dalam fungsi keanggotaan. Didalam semesta penbicaraan (universe of discourse) U. fungsi keanggotaan dari suatu himpunan fuzzy tersebut bernilai antara 0,0 sampaidengan 1.0.
Contoh dari himpunan variable bahasa antara lain:
Himpunan dan suhu atau temperatur dapat dinyatakan dengan: dingin, sejuk, normal, hangat, panas. Grafik dari himpunan suhu ini ditunjukkan pada gambar berikut:

Himpunan dari umur dapat dinyatakan dengan mudah, parobaya, tua, sangat tua.
Grafik dari himpunan ini ditunjukan pada gambar dibawah ini:

Himpunan dari kecepatan dapat dinyatakan dengan: lambat, normal, cepat, sangat cepat. Grafik dari himpunan kecepatan mi ditunjukkan pada gambar:

c. Aritmatika Logika Fuzzy
Dalam system logika fuzzy terdapat beberapa operasi aritmatika yang diperlukan dalam penalarannya antara lain:
a) Gabungan (union) dalam system logika fuzzy dikenal dengan istilah Max.
Operasi max dinyatakan dengan persamaan:

Jika fungsi segitiga dari suatu fungsi keanggotaan adalah A, dan fungsi keanggotaan B adalah trapezium, maka operasi max dari A dengan B ditunjukkan pada gambar 2.7 berikut ini:

b) Irisan (Intersaction) dalam sitem logika fuzzy dikenal dengan istilah Min. operasi mix dinyatakan dengan persamaan:

Jika fungsi A dan B adalah seperti yang ditunjukkan pada gambar 2.7, maka operasi min dari kedua keanggotaan tersebut dapat dinyatakan sebagai berikut ini:

c) Kesamaan (equilary) operasi kesamaan dinyatakan dengan persamaan:

d) Produk (product), operasi produk dinyatakan dengan persamaan:
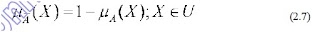
e) Komplemen (complement), operasi komplemen dinyatakan dengan persamaan:

2. BLOCK DIAGRAM FUZZY LOGIC CONTROL
Dalam system control logika fuzzy terdapat beberapa tahapan oprasional yang
meliputi:
1. Fuzzyflkasi
2. Penalaran (Inference Machine)
3. Aturan Dasar (Rule Based)
4. Defüzzyfikasi
Blok diagram control logika fuzzy ditunjukkan pada gambar berikut:

Kerangka operasional control logika fuzzy ditunjukkan pada gambar berikut:

Dari gambar 2.10 sinyal masukan dari KLF dapat berupa nilai tegas. Sinyal masukan KLF dapat diambilkan dari:
a) Selisih antara rujukan (reference) dengan nilai keluaran nyata dan KLF yang berupa nilai kesalahan (errorE).
b) Turunan pertama dan nilai error yang dikenal dengan delta error=dE
3. FUZZYFIKASI
Fuzzifikasi adalah suatu proses pengubahan nilai tegas/real yang ada ke dalam fungsi keanggotaan Misal: merujuk pada gambar 2.1 fuzzifikasi dari suhu35ºc adalah:

Pada gambar 2.11 contoh perhitungan fuzzyfikasi dapat ditunjukkan sebagai berikut:

4. MEMBERSHIP FUNGSI
Fungsi keanggotaan dari suatu himpunan fuzzy dinyatakan dengan derajat keanggotaan suatu nilai terhadap nilai tegasnya yang berkisar antara 0,0 sampai dengan 1,0. Jika A himpunan fuzzy, µA: fungsi keanggotaan dan X: semesta, maka fungsi keanggotaan dalam suatu himpunan fuzzy dapat dinyatakan dengan:
A{(x4tA(x))IxCX}
Fungsi Keanggotaan suatu himpunan fuzzy dapat ditentukan dengan fungsi segitiga (Triangle), trapezium (Trapeoida 1) atau Fungsi Gauss (Gaussian).
Persamaan fungsi keangotaan segitiga adalah:

Persamaan tersebut dalam bentuk grafik ditunjukkan pada gambar berikut:

Persamaan fungsi keangotaan Trapesium adalah:

Persamaan tersebut dalam bentuk grafik ditunjukkan pada gambar berikut:

Persamaan fungsi keanggotaan Gaussian adalah:

Persamaan tersebut dalain bentuk grafik ditunjukkan pada gambar berikut:

5. RULE BASE
Aturan dasar (rule base) pada control logika fuzzy merupakan suatu bentuk aturan relasi implikasi “Jika-Maka” atau “If -Then’ seperti pada pemyataan berikut:
“JIKA” X=A DAN “JIKA” Y=B “MAKA” Z=C
Contoh dari aturan jika-maka ini pada pengendalian suhu ruangan dengan pengaturan kecepatan kipas angin melalui frekuensi variable adalah sebagai berikut:
1. “JIKA” suhu panas DAN
2. “JIKA” kecepatan kipas sangat lambat
3. “MAKA” sumber frekuensi dinaikkan sangat tinggi agar kecepatan kipas tinggi
Jadi aturan dasar KLF ditentukan dengan bantuan seorang pakar yang mengetahui karakteristik objek yang akan kendalikan aturan dasar tersebut dapat dinyatakan dalam bentuk matrik aturan dasar KLF. Contoh aturan dasar dari rancangan pengaturan suhu ruangan dapat dilihat pada table berikut:

6. DEFUZZIFIKASI
Merupakan proses pemetaan himpunan fuzzy ke himpunan tegas (crips). Proses ini merupakan kebalikan dari proses fuzzyfikasi
Proses defuzzyfikasi diekspresikan sebagai berikut:
Z*= defuzzyfikasi (Z)
Dimana :
Z = Hasil penalaran fuzzy
Z* = Keluaran control FL
Defuzzyfikasi = Operasi defuzzier
Metode dalam melakukan defuzzyfikasi antara lain:
1. Metode Max (Maximun)
Metode ini juga dikenal dengan metode puncak dimana nilai keluaran dibatasi oleh fungsi: µc(z*)>µc 1 (z)
2. Metode Titik Tengah (Center ofArea)
Metode ini juga disebut pusat area. Metode ini lazim dipakai dalam proses defuzzifikasi. Metode ini diekspresikan dengan persamaan:

3. Metode Rata-Rata (Average)
Metode ini digunakan untuk fungsi keanggotaan keluaran yang simetris.
Persamaan dan metode ini adalah:

4. Metode Penjumlahan Titik Tengah (Sumarning of center area).
Metode ini dinyatakan dengan persamaan:

5. Metode Titik Tengah Area Terbesar
Dalam metode ini keluaran dipilih berdasarkan titik pusat area terbesar yang ada. Metode ini dinyakan dalam bentuk:

Selanjutnya keluaran keluaran dari defuzzyfikasi tersebut akan digunakan sebagai keluaran KLF.
1. KONSEP FUZZY LOGIC
Sebelum munculnya teori logika fuzzy (Fuzzy Logic), dikenal sebuah logika tegas (Crisp Logic) yang memiliki nilai benar atau salah secara tegas. Sebaliknya Logika Fuzzy merupakan sebuah logika yang memiliki nilai kekaburan atau kesamaran (fuzzyness) antara benar dan salah. Dalam teori logika fuzzy sebuah nilai bisa bernilai benar dan salah secara bersamaan namun berapa besar kebenaran dan kesalahan suatu nilai tergantung kepada bobot keanggotaan yang dimilikinya.
a. Perbedaan Logikafuzzy dengan Logika Tegas
Perbedaan antara kedua jenis logika tersebut adalah: logika tegas memiliki nilai tidak=0.0 dan y=1.0. sedangakan antarn 0.0 hingga 1.0. Secara grafik perbedaan antara logika tegas dan logika fuzzy ditunjukkan oleh gambar dibawah ini:

Didalam gambar 2.1.a) apabila X leblh dan atau sama dengan 10 baru dikatakan benar yaitu bernilai Y1. sebaliknya nilai X yang kurang dan 10 adalah salah yaitu Y=0. Maka angka 9 atau 8 atau 7 dan sejenisnya adalah dikatakan salah.
Didalam gambar 2.1.b) nilai X = 9, atau 8 atau 7 atau nilai antara 0 dan 10 adalah dikatakan ada benarnya dan ada juga salahnya. Dalam contoh kehidupan kita dikatakan seseorang dikatakan sudah dewasa apabila berumur lebih dari 17 tahun. maka sesiapapun yang kurang dari umur tersebut di dalam logika tegas akan dikatakan sebagai tidak dewasa atau anak-anak. Sedangkan dalam hal ini pada logika fuzzy umur dibawah 17 tahun dapat saja dikategorikan dewasa tapi tidak penuh. misal untuk umur 16 tahun atau 15 tahun atau 14 tahun atm 13 tahun. Secara grafik dapat digambarkan sebagai berikut:

b. Himpunan Logika Fuzzy
Dalam teori logika dikenal himpunan fuzzy (fuzzy set) yang merupakan pengelompokan sesuatu berdasarkan variabel bahasa, yang dinyatakan dalam fungsi keanggotaan. Didalam semesta penbicaraan (universe of discourse) U. fungsi keanggotaan dari suatu himpunan fuzzy tersebut bernilai antara 0,0 sampaidengan 1.0.
Contoh dari himpunan variable bahasa antara lain:
Himpunan dan suhu atau temperatur dapat dinyatakan dengan: dingin, sejuk, normal, hangat, panas. Grafik dari himpunan suhu ini ditunjukkan pada gambar berikut:

Himpunan dari umur dapat dinyatakan dengan mudah, parobaya, tua, sangat tua.
Grafik dari himpunan ini ditunjukan pada gambar dibawah ini:

Himpunan dari kecepatan dapat dinyatakan dengan: lambat, normal, cepat, sangat cepat. Grafik dari himpunan kecepatan mi ditunjukkan pada gambar:

c. Aritmatika Logika Fuzzy
Dalam system logika fuzzy terdapat beberapa operasi aritmatika yang diperlukan dalam penalarannya antara lain:
a) Gabungan (union) dalam system logika fuzzy dikenal dengan istilah Max.
Operasi max dinyatakan dengan persamaan:

Jika fungsi segitiga dari suatu fungsi keanggotaan adalah A, dan fungsi keanggotaan B adalah trapezium, maka operasi max dari A dengan B ditunjukkan pada gambar 2.7 berikut ini:

b) Irisan (Intersaction) dalam sitem logika fuzzy dikenal dengan istilah Min. operasi mix dinyatakan dengan persamaan:

Jika fungsi A dan B adalah seperti yang ditunjukkan pada gambar 2.7, maka operasi min dari kedua keanggotaan tersebut dapat dinyatakan sebagai berikut ini:

c) Kesamaan (equilary) operasi kesamaan dinyatakan dengan persamaan:

d) Produk (product), operasi produk dinyatakan dengan persamaan:
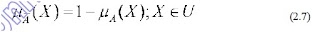
e) Komplemen (complement), operasi komplemen dinyatakan dengan persamaan:

2. BLOCK DIAGRAM FUZZY LOGIC CONTROL
Dalam system control logika fuzzy terdapat beberapa tahapan oprasional yang
meliputi:
1. Fuzzyflkasi
2. Penalaran (Inference Machine)
3. Aturan Dasar (Rule Based)
4. Defüzzyfikasi
Blok diagram control logika fuzzy ditunjukkan pada gambar berikut:

Kerangka operasional control logika fuzzy ditunjukkan pada gambar berikut:

Dari gambar 2.10 sinyal masukan dari KLF dapat berupa nilai tegas. Sinyal masukan KLF dapat diambilkan dari:
a) Selisih antara rujukan (reference) dengan nilai keluaran nyata dan KLF yang berupa nilai kesalahan (errorE).
b) Turunan pertama dan nilai error yang dikenal dengan delta error=dE
3. FUZZYFIKASI
Fuzzifikasi adalah suatu proses pengubahan nilai tegas/real yang ada ke dalam fungsi keanggotaan Misal: merujuk pada gambar 2.1 fuzzifikasi dari suhu35ºc adalah:

Pada gambar 2.11 contoh perhitungan fuzzyfikasi dapat ditunjukkan sebagai berikut:

4. MEMBERSHIP FUNGSI
Fungsi keanggotaan dari suatu himpunan fuzzy dinyatakan dengan derajat keanggotaan suatu nilai terhadap nilai tegasnya yang berkisar antara 0,0 sampai dengan 1,0. Jika A himpunan fuzzy, µA: fungsi keanggotaan dan X: semesta, maka fungsi keanggotaan dalam suatu himpunan fuzzy dapat dinyatakan dengan:
A{(x4tA(x))IxCX}
Fungsi Keanggotaan suatu himpunan fuzzy dapat ditentukan dengan fungsi segitiga (Triangle), trapezium (Trapeoida 1) atau Fungsi Gauss (Gaussian).
Persamaan fungsi keangotaan segitiga adalah:

Persamaan tersebut dalam bentuk grafik ditunjukkan pada gambar berikut:

Persamaan fungsi keangotaan Trapesium adalah:

Persamaan tersebut dalam bentuk grafik ditunjukkan pada gambar berikut:

Persamaan fungsi keanggotaan Gaussian adalah:

Persamaan tersebut dalain bentuk grafik ditunjukkan pada gambar berikut:

5. RULE BASE
Aturan dasar (rule base) pada control logika fuzzy merupakan suatu bentuk aturan relasi implikasi “Jika-Maka” atau “If -Then’ seperti pada pemyataan berikut:
“JIKA” X=A DAN “JIKA” Y=B “MAKA” Z=C
Contoh dari aturan jika-maka ini pada pengendalian suhu ruangan dengan pengaturan kecepatan kipas angin melalui frekuensi variable adalah sebagai berikut:
1. “JIKA” suhu panas DAN
2. “JIKA” kecepatan kipas sangat lambat
3. “MAKA” sumber frekuensi dinaikkan sangat tinggi agar kecepatan kipas tinggi
Jadi aturan dasar KLF ditentukan dengan bantuan seorang pakar yang mengetahui karakteristik objek yang akan kendalikan aturan dasar tersebut dapat dinyatakan dalam bentuk matrik aturan dasar KLF. Contoh aturan dasar dari rancangan pengaturan suhu ruangan dapat dilihat pada table berikut:

6. DEFUZZIFIKASI
Merupakan proses pemetaan himpunan fuzzy ke himpunan tegas (crips). Proses ini merupakan kebalikan dari proses fuzzyfikasi
Proses defuzzyfikasi diekspresikan sebagai berikut:
Z*= defuzzyfikasi (Z)
Dimana :
Z = Hasil penalaran fuzzy
Z* = Keluaran control FL
Defuzzyfikasi = Operasi defuzzier
Metode dalam melakukan defuzzyfikasi antara lain:
1. Metode Max (Maximun)
Metode ini juga dikenal dengan metode puncak dimana nilai keluaran dibatasi oleh fungsi: µc(z*)>µc 1 (z)
2. Metode Titik Tengah (Center ofArea)
Metode ini juga disebut pusat area. Metode ini lazim dipakai dalam proses defuzzifikasi. Metode ini diekspresikan dengan persamaan:

3. Metode Rata-Rata (Average)
Metode ini digunakan untuk fungsi keanggotaan keluaran yang simetris.
Persamaan dan metode ini adalah:

4. Metode Penjumlahan Titik Tengah (Sumarning of center area).
Metode ini dinyatakan dengan persamaan:

5. Metode Titik Tengah Area Terbesar
Dalam metode ini keluaran dipilih berdasarkan titik pusat area terbesar yang ada. Metode ini dinyakan dalam bentuk:

Selanjutnya keluaran keluaran dari defuzzyfikasi tersebut akan digunakan sebagai keluaran KLF.





Tidak ada komentar:
Posting Komentar
Isi Komentarnya Ya